2c3. Composizione dei movimenti: la colubrina
Lo studio realizzato da Galleo riguardante il moto parabolico viene componendo due fondamentali moti fisici: il moto rettilineo uniforme e il moto uniformemente accelerato. La caratteristica principale del moto parabolico consiste nell'essere determinato contemporaneamente da entrambi secondo il principio di composizione dei movimenti. Chiamato anche "legge della indipendente coesistenza dei movimenti in un corpo" o più semplicemente principio di Galileo fu enunciato dallo stesso scienziato all'interno dello scritto Discorsi intorno a due nuove scienze attenenti alla meccanica e ai movimenti locali.
In hac [tractatione], quam modo aggredior, contemplatione, praecipua quaedam symptomata, eaque scitu digna, in medium afferre conabor, eademque firmis demonstrationibus stabilire, quae mobili accidunt dum motu ex duplici latione composito, aequabili nempe et naturaliter accelerata, movetur: huiusmodi autem videtur esse motus ille, quem de proiectis dicimus; cuius generationem talem constituo.
Nella trattazione, che ora comincio, cercherò di presentare, e di stabilire sulla base di salde dimostrazioni, alcuni fenomeni notevoli e degni di essere conosciuti, che sono propri di un oggetto mobile, mentre si muove con moto composto di un duplice movimento, cioè di un movimento equabile e di uno naturalmente accelerato: tale appunto sembra essere quello che chiamiamo moto dei poiettili (lett. “oggetti mandati fuori”); la generazione del quale così stabilisco.
[...]
Proiectum, dum fertur motu composito ex horizontali aequabili et ex naturaliter accelerato deorsum, lineam semiparabolicam describit in sua latione.
Un proiettile (lett. “oggetto mandato fuori”), mentre si muove di moto composto di un moto orizzontale equabile e di un moto naturalmente accelerato, descrive nel suo movimento una linea semiparabolica.
Questo è quello che aveva scoperto Galileo, ora passerò a dimostrare come la traiettoria di un qualsiasi oggetto lanciato in orizzontale o in obliquo sia parabolica. Inizierei il discorso dando una definizione di traiettoria:“si definisce traiettoria di un oggetto la curva geometrica descritta dal corpo durante il sul moto”.Partiamo dal presupposto che la resistenza dell'aria non abbia alcun effetto sul moto del proiettile, quest'ultimo è soggetto alla sola forza gravitazionale. Risulta quindi possibile studiare il moto effettivo di un proiettile come somma degli effetti di due moti immaginari uno verticale, uniformemente accelerato, e l'altro orizzontale, rettilineo uniforme. Il moto orizzontale risulta essere rettilineo uniforme in quanto non consideriamo la presenza dell'attrito causato della presenza di aria; il moto verticaleè uniformemente accelerato perchè dovuto alla sola forza gravitazionale. Prendiamo in considerazione questa immagine:
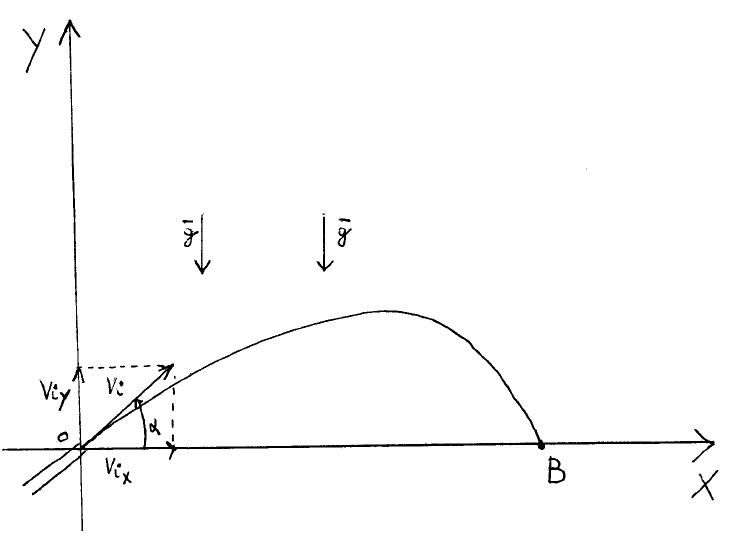
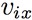: la componente vettoriale 
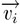sull'asse x
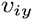: la componente vettoriale 
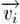sull'asse y
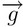: la forza gravitazionale che influisce su x; pari a 0 in quanto 
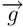è perpendicolare all'asse x
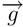: la forza gravitazionale che influisce su y; pari a -9,8 
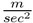.La direzione del vettore accelerazione di gravita viene a formare tra il baricentro del proiettile sparato e il centro della terra. Supponiamo di utilizzare un sistema di riferimento cartesiano ortogonale la cui origine sta nella bocca della colubrina che spara il proiettile. Indichiamo con segno positivo (+) i vettori orientati verso l'alto e con segno negativo (-) quelli orientati verso il basso.
Suddividiamo l'accelerazione gravitazionale nelle componenti cartesiane:
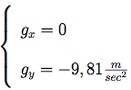
Così facendo siamo in grado di capire alcuni elementi fondamentali per la definire il moto parabolico: dato che l'accelerazione lungo l'asse x è pari a 0 (nulla), questo implica che lungo l'asse x il moto sia rettilineo uniforme; mentre, in virtù della presenza di un'accelerazione costante ( che ricordiamo essere pari a -9,8
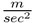), lungo l'asse y troviamo un moto rettilineo uniformemente accelerato.Come conseguenza di questo, troveremo le eqazioni delle velocità e in particolar modo che:
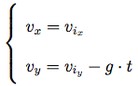
Constatato che sull'asse x si svolgeraì un moto rettilineo uniforme, e sull'asse y un moto rettilineo uniformemente accelerato, assiegnamo per l'asse delle ascisse la legge oraria del moto rettilineo uniforme e per l'asse delle ordinate la legge oraria del moto rettilineo uniformemente accelerato:
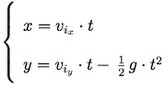
Ora calcoliamo l'equazione del tempo ricavandola dalla prima equazione del sistema:
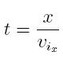
lo sostituiamo all'interno della seconda equazione del sistema:
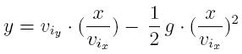
svolgiamo le operazioni e riordiniamo secondo la forma canonica:
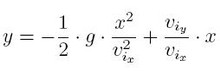
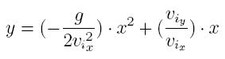
A questo punto abbiamo finito, in quanto le quantità g, v/ix, v/iy sono dati iniziali del problema e quindi costanti. In questo modo l'equazione può essere ridotta alla forma y = ax+ bx + c che si da il caso sia l'equazione canonica della parabola. Consultando la dimostrazione alternativa, potrete accedere ad una dimostrazione più approfondita del moto parabolico dei proiettili
In questo video possiamo notare come vengano raffigurati tre diversi moti di un proiettile, sparati da una colubrina, cannone di piccole dimensioni diffusosi in Italia fin dallaseconda metà del XVI secolo.
Prima animazione: ho voluto rappresentare come si pensava avvenisse il moto di un proiettile nell'opinione comune prima della scoperta galileiana che rivelava la sua natura parabolica: allora si riteneva che un proiettile continuasse a muoversi lungo la sua traiettoria iniziale, obliqua o orizzontale che fosse, fino all'esaurimento della forza con cui era stato lanciato; quando questa forza si esauriva, il proiettile cadeva perpendicolarmente verso il suolo.
Seconda animazione: viene rappresentato il moto parabolico di un proiettile come lo aveva pensato Galileo e come effettivamente è.
Terza animazione: viene esposta infine la teoria di Galileo racchiusa nelle parole di Sagredo all'interno del "Dialogo sopra i due massimi sistemi, Tolemaico e Copernicano" :
“[...] Quando in cima di una torre fusse una colubrina livellata, e con essa si tirassero tiri di punto bianco, cioè paralleli all'orizonte, per poca o molta carica che si desse al pezzo, sí che la palla andasse a cadere ora lontana mille braccia, or quattro mila, or sei mila, or dieci mila etc., tutti questi tiri si spedirebbero in tempi eguali tra di loro, e ciascheduno eguale al tempo che la palla consumerebbe a venire dalla bocca del pezzo sino in terra, lasciata, senz'altro impulso, cadere semplicemente giú a perpendicolo.”
E cioè che il tempo impiegato da un proiettile, sparato ad una qualsiasi velocità, per arrivare al suolo è il medesimo di un proiettile lasciato cadere dallo stesso punto in cui l'altro è stato sparato senza alcuna spinta.
Si veda anche il contributo di C. Jarach.