2c3. Dimostrazione alternativa (più corretta ed approfondita)
Partiamo dal presupposto che la resistenza dell'aria non abbia alcun effetto sul moto del proiettile, quest'ultimo è soggetto alla sola forza gravitazionale. Risulta quindi possibile studiare il moto effettivo di un proiettile come somma degli effetti di due moti immaginari: uno verticale, uniformemente accelerato; e l'altro orizzontale, rettilineo uniforme. Il moto orizzontale risulta essere rettilineo uniforme in quanto non consideriamo la presenza dell'attrito causato della presenza di aria; il moto verticale è uniformemente accelerato perchè dovuto alla sola forza gravitazionale.
Trascurare l'effetto della resistenza dell'aria è accettabile per velocità del proiettile limitate. Considerare costante l'accelerazione di gravità è allo stesso modo accettabile per un'altezza massima della traiettoria anch'essa limitata.
Scegliamo il piano XY coincidente con il piano definito dai vettori:
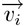(velocità iniziale del proiettile) e
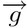(accelerazione di gravità) applicati al baricentro del proiettile
L'origine O degli assi cartesiani ortogonali coincide con la bocca di uscita della colubrina (mezzo di lancio del proiettile): l'asse Y è diretto verso l'alto e l'asse X nel senso del moto.
Le componenti dei vettori sono:
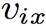: la componente vettoriale 
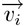sull'asse x
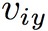: la componente vettoriale 
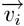sull'asse y
gx: la forza gravitazionale che influisce su x; pari a 0 in quanto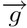 
è perpendicolare all'asse x
gy: la forza gravitazionale che influisce su y; pari a -9,8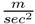 
.
Il moto del proiettile può essere scomposto in un moto orizzontale rettilineo uniforme con velocità costante e in un moto verticale rettilineo uniformemente accelerato con accelerazione costante pari a -9,8 e velocità iniziale nulla.
Come detto prima, moto orizzontale e moto verticale sono indipendenti uno dall'altro, non si influenzano vicendevolmente e possono pertanto essere trattati separatamente senza seguire l'effettiva traiettoria parabolica del proiettile.
Applicando le equazioni del moto rettilineo uniforme al moto orizzontale del proiettile e quelle del moto rettilineo uniformemente accelerato al moto verticale otteniamo:
(1) 
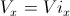
(2) 
(3) 
(4) 
L'equazione y = f(x) della traiettoria del proiettile si ottiene ricavando t dalla (3) e sostituendo il risultato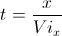 
nella (4)
Quest'ultima diviene dunque
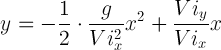
Questa è l'equazione di una parabola
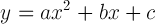con i seguenti parametri: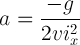
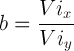
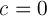
Il grafico della traiettoria del proiettile è anche quello dell'equazione del moto verticale uniformemente accelerato del proiettile stesso. In questa immagine (fig. 1) è rappresentata la traiettoria parabolica y = f(x) il cui moto è definito dai seguenti dati:
, 
, 
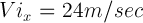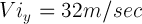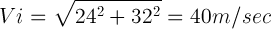
Le caratteristiche del moto parabolico descritto dal proiettile sono dunque le seguenti:
L'angolo alpha formato da Vi con l'asse X (definito alzo del proiettile) è di circa 53°;
Le coordinate del punto M, punto di massima altezza nonchè vertice della parabola, e Mx e My sono pari rispettivamente a 78,37 m e 52,24 m.;
La gittata R è doppia rispetto al valore di Mx e di conseguenza pari a 156,73m;
Il tempo impiegato per raggiungere M risulta essere:
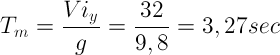
Il tempo di volo (impiegato per tornare alla quota di lancio pari a 0) è
