2a5. Argomenti certissimi dell'immobilità della Terra: i tiri di artiglieria
Introduzione
Il testo riportato appartiene alla più famosa opera di Galilei: il “Dialogo sopra i due massimi sistemi del mondo”. L'opera fu pubblicata nel 1632 a Firenze con lo scopo, sebbene in parte edulcorata dall'intervento della censura ecclesiastica, di dimostrare la verità del sistema eliocentrico copernicano in opposizione a quello geocentrico della tradizione aristotelico-tolemaica. I personaggi presenti nell'opera sono tre:
Simplicio: professore aristotelico e sostenitore del modello geocentrico;
Salviati: accademico fiorentino favorevole al modello copernicano e portavoce delle idee di Galilei;
Sagredo: aristocratico veneziano, appassionato delle scienze e sostenitore del modello copernicano.
Sintesi del brano
Simplicio e Salviati stanno discutendo intorno alle prove dell'immobilità della terra.
Simplicio afferma che, se la terra si muovesse, i tiri d'artiglieria diretti ad est, ovvero nello stesso verso del moto di rivoluzione terrestre, dovrebbero risultare più corti di quelli rivolti a ovest perché nel primo caso il moto terrestre avvicina il cannone al punto di arrivo del proiettile mentre nel secondo caso lo allontana.
Salviati, discordando, lo sfida a trovare un esperimento corrispondente, come era stato nel caso del moto di caduta libera della palla dalla torre, che possa permettere di appurare chi dei due abbia ragione. Sagredo propone di prendere in considerazione il caso di una carrozza scoperta che procede, secondo i termini della fisica moderna, per un moto rettilineo uniforme e dalla quale siano scagliate due frecce: una nello stesso verso in cui si muove la carrozza, l'altra in quello opposto; e, tenendo conto della posizione della carrozza al momento in cui la freccia si conficca nel terreno, misurare la distanza tra la freccia e la carrozza, ovvero il tiro.
Il movimento della carrozza rappresenterebbe quello della terra, e la freccia la palla di cannone.
Simplicio sostiene che il tiro della freccia scagliata nel verso del moto della carrozza sarà più corto dell'altro perché la carrozza si è avvicinata alla freccia nel primo caso e allontanata nel secondo.
Salviati gli fa notare che bisogna tener conto del fatto che la carrozza, così come tutto quello che vi è sopra (balestriere, balestra e freccia), sono già in movimento al momento del tiro e quindi alla velocità impressa alla freccia dalla balestra bisogna sommare o sottrarre a secondo del verso in cui avvenga il tiro anche la velocità impressa dalla carrozza in movimento. Così, nel caso di un tiro nel verso in cui si muove la carrozza, l'avvicinamento del veicolo sarà compensato da una maggiore velocità della freccia e il tiro risulterà quindi uguale a quello di una freccia scagliata nel verso contrario perché, sebbene la carrozza si allontani da essa, avrà una velocità minore. Lo stesso, continua Salviati, vale per i tiri di cannone che, anche se la terra si muovesse, risulterebbero di uguale lunghezza in entrambe le direzioni a patto che venga applicata uguale forza. Simplicio, incredulo, replica chiedendo come è possibile che avvenga questo movimento della terra senza che nessuno se ne accorga. Salviati risponde che, siccome anche noi e tutto ciò che ci circonda ci muoviamo con la terra, non abbiamo punti di riferimento per notare questo moto (secondo il principio della relatività galileiana).
Bisogna notare che il testo tratto dai Discorsi non prova direttamente il movimento della terra ma afferma che in linea di principio è possibile, confutando le prove (definite ironicamente da Galileo “certissimi argomenti”) che negavano a prescindere questa tesi. In realtà Galilei crede nell'assoluta verità dell'eliocentrismo ma non lo esprime esplicitamente a causa delle restrizioni imposte dall'Inquisizione dopo il 1616.
La composizione delle velocità
In questo testo Galilei introduce il concetto di composizione delle velocità che serve a calcolare la velocità complessiva di un oggetto quando è sottoposto a più moti contemporaneamente.
Enunciato:
Prendendo in considerazione un corpo soggetto a due movimenti simultanei, il primo a velocità v e il secondo a velocità u, la velocità complessiva del corpo, detta w, è la somma vettoriale di v e u: w=u+v.
Applicazione
Facciamo l'esempio di un uomo che corra alla velocità di 2 m/s sul ponte di una nave che procede alla velocità di 8 m/s. Qual è la velocità complessiva dell'uomo?
Dobbiamo anzitutto considerare le velocità come velocità vettoriali: poniamo che la nave si muova nel verso positivo della retta orientata. Ora se il nostro uomo procede lungo la retta nel verso positivo avremo w=8+2; w=10. Se procede in verso opposto la sua velocità sarà un vettore di verso negativo e avremo w=8-2; w=6. Se il movimento avviene in diagonale basterà calcolare il risultante tra i due vettori mediante il metodo testa-coda.
Esercizi sulla composizione delle velocità
Due treni A e B viaggiano su binari paralleli, in versi opposti, con velocità di modulo VA=90km/h e VB=60 km/h. Mentre i due treni si incrociano, un viaggiatore sul treno A lancia orizzontalmente una bottiglia dal finestrino, perpendicolarmente al treno, con modulo della velocità u=30km/h. Si determini il modulo della velocità U della bottiglia per un viaggiatore sul treno B.
Risoluzione:
Partiamo dal presupposto che al viaggiatore sul treno B la bottiglia sembrerà giungere più velocemente della sua velocità effettiva (che è il vettore ipotenusa del triangolo rettangolo formato unendo VA- la velocità del treno da cui è lanciata- e u-la velocità con cui è lanciata) in virtù del fatto che egli si muove in direzione opposta a quella del treno A: quando due treni si incrociano, il passeggero, non avendo più punti di riferimento fissi (dal finestrino vede solo il treno di fronte che sfreccia), avrà la sensazione di essere fermo e che l'altro treno si muova velocissimo, precisamente a una velocità che è la somma delle velocità dei due treni. Per questo per calcolare la velocità della bottiglia percepita dal viaggiatore bisognerà considerare un sistema di riferimento solidale al treno B, calcolare per la legge di composizione delle velocità il vettore Vc che è il vettore somma di VAe VB e sommarlo al vettore della velocità u, ottenendo il vettore della velocità percepita U:

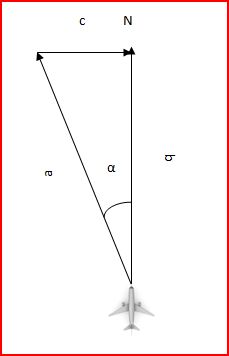
Un aereo deve raggiungere una località situata a 1152 km a nord rispetto al punto di decollo. La sua velocità di crociera, valutata rispetto all'aria ferma, è 170 m/s. Il pilota osserva che, per muoversi secondo la direzione nord, l'aereo deve puntare secondo una direzione che forma un angolo di a gradi verso sinistra. Supponendo che questo orientamento sia determinato da un vento che soffia costantemente da sinistra a destra, se ne determini la velocità sapendo che il viaggio dura esattamente 2 ore.
Risoluzione:
L'aereo procede a 170 m/s su una direzione che forma un angolo di a gradi verso sinistra (vettore a) ma alla fine è come se avesse proceduto alla velocità di 160 m/s sulla direzione nord (vettore b) perché impiega due ore al posto dei 112 minuti previsti in condizioni ottimali (ovvero procedendo a 170 m/s in direzione nord). Questo perché interviene un vento che tende a spingerlo verso destra e dunque l'aereo deve dirigersi più a sinistra per ritrovarsi perfettamente nel punto d'arrivo previsto.
Per la legge della composizione delle velocità la velocità del vento si trova calcolando il vettore c che unisce i vertici dei due vettori a e b: