2a5. Argomenti certissimi dell'immobilità della Terra: i tiri d'artiglieria
Sintetizza il brano evidenziando attraverso quale paragone e con quale ragionamento Salviati sostiene che neppure i tiri di artiglieria possono essere considerati una prova dell’immobilità della Terra.
In questa parte del “Dialogo” Galileo confuta una delle prove più famose degli aristotelici a favore dell'immobilità della Terra, quella riguardante i tiri di artiglieria. Grazie al paragone della freccia lanciata da una carrozza in corsa, Galileo dimostra come non sia valida la considerazione degli aristotelici per cui la Terra doveva necessariamente essere ferma. Ammessa la rotazione, il proiettile una volta lanciato conserva il suo movimento in direzione est, movimento che gli appartiene quando è ancora sulla superficie terrestre, e non in aria. Il movimento nella stessa direzione della carrozza e nella direzione opposta si compone dunque con il movimento in direzione est: in tal modo il proiettile mantiene sempre la propria posizione relativamente alla superficie terrestre, e quindi al bersaglio. Salviati dunque grazie al paragone con una carrozza in corsa dimostra a Simplicio che neanche questa considerazione sui tiri d'artiglieria è una prova dell'immobilità della Terra.
Simplicio sosteneva che, se si fosse supposta la rotazione, un tiro verso levante sarebbe risultato assai più corto dell'opposto tiro verso occidente. Al contrario invece i tiri sarebbero risultati di eguale misura, come è. Salviati invece gli spiegherà che, anche ammettendo il movimento della terra, i due tiri sono uguali.
Si prenda una carrozza scoperta, dice Salviati, e si posizioni in essa un balestrone da bolzoni (1) a mezza elevazione, in modo che il tiro risulti più lungo possibile, e si lanci una freccia prima nella direzione di marcia, poi, in una seconda corsa, in senso contrario. In questo modo si possono paragonare i due lanci su un percorso della medesima durata e con un lancio di medesima ampiezza. Simplicio è d'accordo nel fare l'esperimento, sostenendo ancora che il tiro (lo spazio tra la freccia e dove si trova la carrozza nel momento in cui la freccia si ficca a terra) sarà minore quando si tira verso il corso della carrozza.
“Sia, per esempio, il tiro in se stesso trecento braccia, e 'l corso della carrozza, nel tempo che il bolzone sta per aria, sia braccia cento: adunque, tirandosi verso il corso, delle trecento braccia del tiro la carrozzetta ne passa cento, onde nella percossa del bolzone in terra lo spazio tra esso e la carrozza sarà braccia dugento solamente; ma all'incontro nell'altro tiro, correndo la carrozza al contrario del bolzone, quando il bolzone arà passate le sue trecento braccia e la carrozza le sua cento altre in contrario, la distanza traposta si troverà esser di braccia quattrocento.”
Supponiamo di voler effettuare un tiro di 300 braccia, e che, durante il volo della freccia, la carrozza compia 100 braccia. Tirando verso il corso della carrozza, il tiro (spazio tra la freccia e dove si trova la carrozza nel momento in cui la freccia si ficca a terra) risulta di 200 braccia, nell'altro caso 400.
Per Simplicio l'unico modo per far risultare i due tiri uguali sarebbe quello di lasciare ferma la carrozza, il che spiegherebbe l'immobilità della Terra. Ma Salviati gli dimostra che non è così: si potrebbe “ingagliardire” (rafforzare) il primo arco (quello che va secondo il corso della carrozza) e “indebolire” il secondo. Ma di quanto? Nel nostro esempio, avendo supposto un tiro di 300 braccia, bisognerebbe per il primo arco, ingagliardirlo perché percorra 400 braccia, e l'altro indebolirlo perché ne compia 200, in maniera tale che raggiunga il risultato di 300 nel primo caso, sottraendo le 100 braccia compiute dalla carrozza, nel secondo aggiungendole. Salviati è quasi riuscito a dimostrare a Simplicio che si sbaglia:
“SALV.: Ma che effetto fa nella freccia la maggior o minor gagliardia dell'arco?
SIMPL.: L'arco gagliardo la caccia con maggior velocità, e 'l piú debole con minore; e l'istessa freccia va tanto piú lontana una volta che l'altra, con quanta maggior velocità ella esce della cocca l'una volta che l'altra.
SALV.: Talché per far che la freccia tirata tanto per l'uno quanto per l'altro verso s'allontani egualmente dalla carrozza corrente, bisogna che se nel primo tiro dell'esempio proposto ella si parte, verbigrazia, con quattro gradi di velocità, nell'altro tiro ella si parta con due solamente. Ma se si adopra il medesimo arco, da esso ne riceve sempre tre gradi.”
Tirando con il medesimo arco i tiri non possono quindi risultare uguali?
Non abbiamo però considerato con che velocità corra la carrozza, dice Salviati.
La carrozza nel nostro caso si muove con una velocità di 1 grado, avendo supposto quella dell'arco uguale a 3. La carrozza si muove quindi con una velocità di 1 grado: la carrozza e tutto quello che la carrozza contiene, freccia, arco, corda inclusi.
Dunque:
Nello scaricare la freccia verso il corso della carrozza l'arco imprime i suoi 3 gradi di velocità ad una freccia che ne ha già 1, quindi la freccia esce dalla corda che ne ha 4. Nel secondo caso invece il medesimo arco conferisce i suoi 3 gradi ad una freccia che si muove con una velocità di -1, arrivando quindi a terra con una velocità di 2 gradi. Salviati dunque mostra a Simplicio che i due tiri sono uguali, avendo quest'ultimo affermato che lo sarebbero stati se la freccia fosse uscita una volta con 4, l'altra volta con 2 gradi. Come per la carrozza anche per l'artiglieria:
“[…] muovasi la Terra o stia ferma, i tiri fatti dalla medesima forza hanno a riuscir sempre eguali, verso qualsivoglia parte indrizzati.”
Simplicio non è ancora convinto: se la terra si muove orizzontalmente, perché io vedo dei moti perpendicolari e retti? Semplice, dice Salviati, poiché tutto si muove, noi compresi, quindi il movimento risulta impercettibile ai nostri sensi, ma c'è.
(1) Un balestrone da bolzoni era una balestra che lanciava una freccia chiamata bolzone, dardo munito all'estremità di capocchia al posto della punta.
Enuncia il principio di composizione delle velocità e mostrane alcune applicazioni.
Si può quindi facilmente enunciare il principio di composizione della velocità:
Un corpo soggetto a due movimenti simultanei, il primo con velocità v1, il secondo con una velocità v2, ha una velocità compessiva vTOT data dalla somma vettoriale delle due velocità.
La somma vettoriale w=u+v con:
u= velocità di un corpo x rispetto ad un corpo y;
v= velocità di y rispetto ad un corpo z;
Nel nostro primo caso, supponendo x= la freccia, y= la carrozza, z= il suolo, u=3 e v=1, abbiamo che
W= 3+1
W= 4
Nel secondo invece, x y e z sono le medesime ma v è l'opposto.
Quindi:
W'= 3-1
W'= 2
Una possibile applicazione del principio di composizione della velocità, sarebbe quella di determinare la velocità necessaria per un nuotatore nel momento in cui quest'ultimo si dovesse trovare a nuotare controcorrente.
Supponiamo ad esempio che Carlotta sia capace di nuotare alla velocità di 1,5 m/s rispetto all'acqua. Ella si trova a nuotare in un fiume, in cui la corrente ha una velocità di 1 m/s rispetto alla riva (ho volutamente parlato di fiume e non di mare, poiché prendere come punto di riferimento la riva che è ferma è meglio rispetto ad una barca in mare aperto che, seppur leggermente, si muove). Un problema potrebbe consistere nel determinare le velocità di Carlotta rispetto alla riva, se nuota nella direzione e verso della corrente e se nuota controcorrente.
Il problema si potrebbe facilmente risolvere applicando il principio di composizione delle velocità.
Vediamo ora il procedimento:
Carlotta è la nostra x. La nostra y è l'acqua, e la nostra z è la riva del fiume.
Essendo v= 1 m/s e v'= -1 m/s e u= 1,5 m/s avremo:
w= 2.5 m/se w'= 0.5 m/s. w è la velocità di Carlotta se ella nuota secondo la corrente, w' se nuota controcorrente.
Due treni A e B viaggiano su binari paralleli, in versi opposti, con velocità di modulo vA=90km/h e vB=60 km/h. Mentre i due treni si incrociano, un viaggiatore sul treno A lancia orizzontalmente una bottiglia dal finestrino, perpendicolarmente al treno, con modulo della velocità u=30km/h. Si determini il modulo della velocità U della bottiglia per un viaggiatore sul treno B.
Risoluzione:
La velocità della bottiglia in un sistema di riferimento solidale con il viaggiatore che si trova sul treno B è data dal vettore risultante tra il vettore somma vA+vB (vC) e il vettore della velocità u.
vC=90km/h + 60 km/h= 150 km/h
U=153km/h
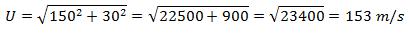
Risoluzione:
L'aereo procede a 170 m/s su una direzione che forma un angolo di a gradi verso sinistra (vettore a) ma alla fine è come se avesse proceduto alla velocità di 160 m/s sulla direzione nord (vettore b) perché impiega due ore al posto dei 112 minuti previsti in condizioni ottimali (ovvero procedendo a 170 m/s in direzione nord). Questo perché interviene un vento che tende a spingerlo verso destra e dunque l'aereo deve dirigersi più a sinistra per ritrovarsi perfettamente nel punto d'arrivo previsto.
Per la legge della composizione delle velocità la velocità del vento si trova calcolando il vettore vC che unisce le punte dei due vettori a e b:
c=57.44 m/s
